こんにちは、けいタンです。今週の月曜日に基礎英単語24選というもの投稿しました。
・知っていなきゃまずい基礎英単語24選~まずはここから (keitan-zatsugaku.com)
今日からも新しく週一回のペースで英語とは違う分野の勉強コンテンツを発信しようと思います。
今週から毎週水曜日、高校数学の問題を取り上げます!
そのテーマは、タイトルにもある通り「数学」(一応、高校数学がメイン)です。
なぜこのテーマにしたかというと先日、自分の部屋の片づけをしていたらあるプリント集が見つかりました。
見てみると私が少し前にアルバイトとして働いていた塾での高校生向けの数学対策のプリントでした。
ちなみに、このプリント集は私が作ったものなんです。
塾はもう辞めましたし、捨てるべきか迷いました。
ですが、このような形で雑学系・勉強系のブログを開くことにしたので勉強コンテンツの一環として利用しようと考えました。
どんな内容のものをするのか?
先ほども述べましたが基本的には高校数学(数学ⅠA・ⅡB・Ⅲ)を取り上げるつもりです。
また、私は大学でも数学を勉強しているので大学数学も時折入れていこうかなと思います。
しかしそれでは、数学が苦手な方にとってはキツイと感じる方もいるかもしれません。
だから、たまに数学が苦手な人でも取り組めるような面白い数字ゲーム(パズル)を行おうと思います。
なので、数学が苦手だと思う方は数字ゲーム(パズル)だけでもいいので遊びに来てくださいね!
それでは、そろそろ今日の問題を私と一緒に見てみましょう!
今日の問題~高校数学Ⅰ 2次関数の場合分け(難易度☆…簡単)
aは正の定数とする。
定義域が0≦x≦aである 関数y=x²-4x+1の最大値と最小値を次の各場合について求めよ。
(1) 0<a<2 (2)2≦a<4 (3)a=4 (4) 4<a
問題解決のためのヒント
2次関数の最大最小を求める標準的な問題ですね。
まずは平方完成してから問題に沿って場合分けをしていきましょう。
グラフは面倒かもしれませんがそれぞれの場合ごとに書いた方がいいです。
今回の問題では、場合分けの基準が問題に示されているのでその点については大丈夫です。
が、一般的に場合分けの基準は「頂点と区間の両端の値を比較して考える」ことが主です。
場合分けの考え方は大切なので今回の問題をいい機会として理解しておきましょう。
まずは分からなくても、できなくてもいいので時間をかけてゆっくりじっくり問題について考えてみてください。
その思考にかけた時間だけ成長できます。
問題の解答
グラフを書く必要があるので画像で解答を示します。(見えにくいところがあったらスミマセン)
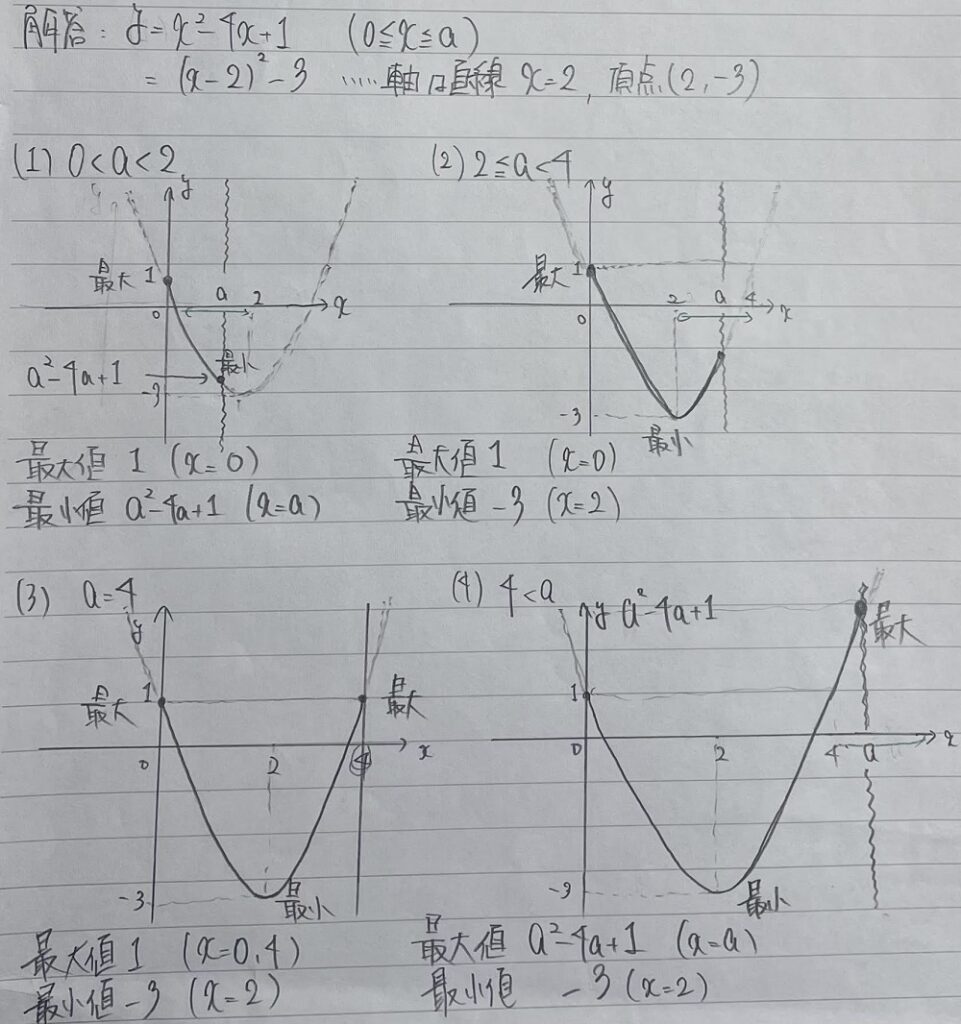
以上になりますが、どうだったでしょうか?
こんな感じで塾講師時代に使っていたプリントを使って高校数学を解説していこうと思います。
では少し長くなりましたので今日はここまでにしますね。
最後までお付き合いくださりありがとうございました。ではまた明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)


