こんにちは、けいタンです。
今日も前回に引き続いて高校数学の問題演習を行います。
今回の問題ジャンルについて
今回は「数Ⅱの因数定理と高次方程式」という問題をします。
中学校の数学では、xの1次方程式やxの2次方程式を解くことをやりました。
そして、高校数学レベルにもなると、3次方程式や4次方程式などといった
高次な方程式を解くことになります。
そこで今回は、高次方程式を簡単なものから、因数定理を使ったちょっとだけ面倒なもの
までの問題を解く練習をしましょう!
なので、因数定理や高次方程式が苦手な方も嫌いな方も、数学が得意になりたい方も
考えるだけでもいいので、問題を見てみてぜひ、チャレンジしてみてください!!
それが数学ができるようになるきっかけの一つとなれるかもしれませんからね!
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:数学パズル第3回~意外と解けない虫食い算に挑め!
↑分かっている情報から分からないところを推測して解く虫食い算に挑戦してみませんか?地味に好評の数学パズル第3弾!

・合わせて読むべき関連記事:高校数学~数Ⅲ正三角形と複素数平面
↑ここでは、数Ⅲの正三角形と複素数平面の問題について取り上げます。数学が苦手な方や得意になりたい方は一度、見てほしいと思います。
・合わせて読むべき関連記事:数学パズル~騙されるか騙されないか
↑こちらでは、ちょっと頭を使わないといけない面白い数学パズルのクイズを紹介しています。
あなたは嘘つき者やいいかげんな者に騙されることなくパズルを解くことができるでしょうか??
外出せず3時間で履歴書に書ける資格がとれる!伝え方コミュニケーション検定
![]()
↑自己肯定感が上がれば、自分の未来や将来の生き方が良くなるかも…
とにかく、ネガティブな考えよりもポジティブでありたいものですよね!
では早速、因数定理と高次方程式の問題について見ていきましょう!
今回の問題~数Ⅱ 因数定理と高次方程式(難易度☆☆…簡単・標準)
問題:数Ⅱー因数定理と高次方程式
次の高次方程式を解け。
- x³=27
- x⁴-x²-6=0
- x⁴+x²+4=0
- x³+3x²+4x+4=0
- 2x⁴+5x³+5x²-2=0
↑初心者からAIエンジニアになりたい方必見のオンラインAIプログラミングスクールです。
プログラミングも小学校で必修になりましたし、今からでもプログラミングを学習してみませんか?
問題解決のためのヒント
1番については、これは3次の因数分解で解けますよね。
x=3だけが答えではないので、気を付けてくださいね。(解は3つある)
2番は、置換すれば簡単な2次方程式に直せます。
すなわち、x²=Xとおいて考えるのです。
そうしてあとは、因数分解から4次方程式の解xが求まることでしょう。
意外と解けそうで解けないのが3番かと思います。
なぜなら、2番と同じようにx²=Xと置いたところで、うまく因数分解できないからです。
なのでここでは、「和と差の積」を利用しましょう!
つまりどういうことかといいますと、
x⁴+x²+4=0 を
(x²+2)²-3x²=0と変形し、
2乗ひく2乗の形を半ば強引に作るのです。
そして、和と差の積による因数分解を行えば、大丈夫でしょう。
4番・5番については、因数定理を使わないといけません。
4番についてまずは、(左辺)=0となるようなxの値を見つけましょう。
おそらく、x=-2が一番見つけやすい解の1つだと思います。
その後は、組立除法を行うことで1次式と2次式に因数分解することができますので、
xの値も求められます。
5番も因数定理を2回使うところ以外の解法は4番とことさら変わりないので、
残りは自力で頑張ってくださいね!
問題の解答
毎度のこと自分なりに分かりやすく手書きで作った解答を画像で示します。
一度自分なりにある程度解いてから、答えを確認するとより理解が深まりますよ。
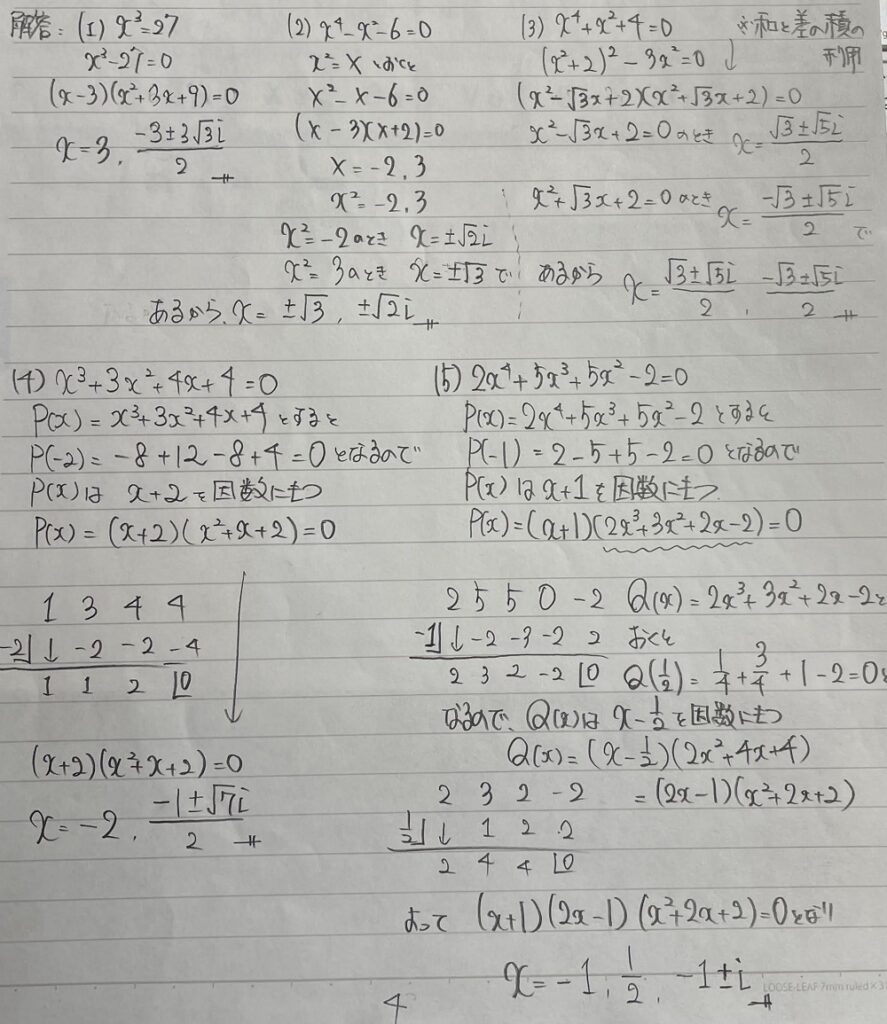
どのような過程で問題を解いているのかをしっかりと確認してくださいね!
まとめ~他の問題もいろいろ解いてみよう!
皆さん、やってみてどうだったでしょうか。
今回は高次方程式を因数定理や置換・和と差の積を利用して因数分解することが分かれば、
確実に解けた問題だったと思います。
とにかく、大切なことは実際に問題を解いてみて、どこが分からないのか。どこができないのか…
というように、いろいろ自分なりに考えて、そして自分の手で問題を解くことが何より、
数学ができるようになるための一つのステップになります。
あと、最後まで解けた方は高次方程式(置換・因数定理)の基本的な問題については大丈夫なので、
この調子でほかの高次方程式の問題やほかの分野についても頑張っていきましょう!
また、最後まで解けなかった方も今回をいい機会として、
いろいろ自分なりに復習してほしいと思います。
あきらめずにコツコツ継続して学習することが最短の学力向上につながります!
「急がば回れ」の考え方ですよ~!
いいね!とシェアによるこのブログの拡散をお願いします!
今回の内容で少しでも面白い・タメになると感じてくれたら嬉しいです。
そして、
面白い・タメになると思った方は、いいね!とシェアによるこのブログの拡散をお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では、今回はここまでにします。
最後まで見ていただきありがとうございました。
![]()
↑なんと現在、こどもちゃれんじ・進研ゼミ小学/中学/高校講座にて「4月号、実質無料キャンペーン」を開催しているそうです!!このチャンスを逃すな!!
気になる方はチェックして内容を確認するだけでもしてみよう。
また、明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
・合わせて読むべき前回の関連記事:数学パズル第3回~意外と解けない虫食い算に挑め!
↑分かっている情報から分からないところを推測して解く虫食い算に挑戦してみませんか?地味に好評の数学パズル第3弾!
・合わせて読むべき関連記事:高校数学~数Ⅲ正三角形と複素数平面
↑ここでは、数Ⅲの正三角形と複素数平面の問題について取り上げます。数学が苦手な方や得意になりたい方は一度、見てほしいと思います。
・合わせて読むべき関連記事:数学パズル~騙されるか騙されないか
↑こちらでは、ちょっと頭を使わないといけない面白い数学パズルのクイズを紹介しています。
あなたは嘘つき者やいいかげんな者に騙されることなくパズルを解くことができるでしょうか??



コメント