こんにちは、けいタンです。
今週も元気よく頑張って数学の問題を一問解きましょう。
今回は数Ⅱの対数関数の不等式の問題を行います。
今日扱う、この問題は対数関数の基本的な定理や仕組みがいろいろと関係しています。
なので、解くことだけでも対数関数について理解・復習できる良問だと思いますので10分間だけお時間をくださいね!
そして、対数関数が苦手な方も数Ⅱが苦手な方も、そもそも数学が苦手な方も私と一緒に数学ができるようになるきっかけの一つとなれるよう頑張りましょう!
・合わせて読みたい前回の関連記事:高校数学第3回~数Ⅱ指数関数の不等式(難易度☆☆)~022(数学③) – (keitan-zatsugaku.com)
今回の問題~数Ⅱ対数関数の不等式(難易度☆☆☆…やや難)
今回も画像で問題を示します。見えにくかったらスミマセン。
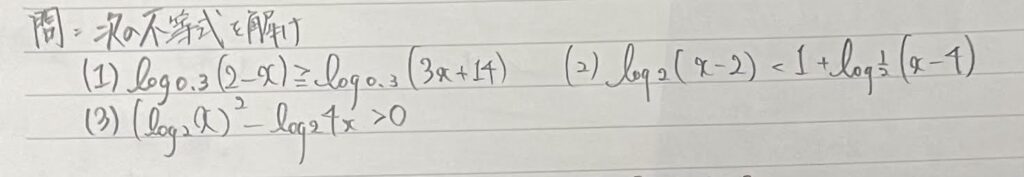
問題解決のためのヒント
標準的な問題ですが(2)と(3)は、工夫して考えないと少々難しい問題です。
前回の指数関数の不等式を解くときには、底をそろえることが最も大切だといいましたが、
対数関数の不等式の解法にも全く同じことがいえます。
すなわち、まずは底をそろえるところから始まるというわけです。
面白いことに指数関数と対数関数の不等式の解法には似たところが多くあります。
よって、底をそろえてそのあとは、対数の真数部分について不等式を解けばいいのです。
そして指数関数の不等式同様、一つだけ気を付けておきたいことがありましたね。
それは、底が1より小さい場合は不等号の向きを反対にしないといけないことです。
思い出せたでしょうか?
忘れていた方は気を付けておきましょうね。
この問題だと(1)が該当します。
また、(3)は置換して考えた方がいいでしょう。
あと最後に1つだけ忘れやすい定理なのですが、
真数条件というものがありましたよね。
真数条件では、真数>0になるので注意してください。
ちなみに(2)では、底をそろえないといけませんよね。
そんな時には、底の変換公式を用いる必要があります。
今話題のSTEM教育【Groovy Lab in a Box】
![]()
問題の解答
毎度のこと自分なりに分かりやすく手書きで作った回答を画像で示します。
一度自分なりにある程度解いてから、答えを確認するとより理解が深まりますよ。

どうだったでしょうか。
しっかり考えないと解けない問題だったと思います。
大切なことは実際に問題を解いてみて、どこが分からないのか。どこができないのか…
というように、いろいろ自分なりに考えて、そして自分の手で計算を行うことが何より、数学ができるようになるための一つのステップなのです。
あと、最後まで解けた方は対数関数の不等式の問題に関してはもうバッチリなので、
この調子でほかの分野についても頑張っていきましょう!
また、最後まで解けなかった方も今回をいい機会としていろいろ自分なりに復習してほしいと思います。
あきらめずにコツコツ学習することが最短の学力向上につながります!
今回の内容で少しでもタメになると感じてくれたら嬉しいです。
そして、
面白い・タメになると思った方は、いいね!とシェアによるこのブログの拡散をお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では、今回はここまでにします。
最後まで見ていただきありがとうございました。
また、明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
・合わせて読みたい前回の関連記事:高校数学第3回~数Ⅱ指数関数の不等式(難易度☆☆)~022(数学③) – (keitan-zatsugaku.com)


