こんにちは、けいタンです。
今週も元気よく頑張って数学の問題を一問解きましょう。
今日がこのけいタンのブログの50回目の投稿になります。
ということは、けいタンのブログ開設から50日経ったということになりますが、
あっという間でとてつもなく早いものですね。
今後も、「1日1つだけ5分間の学び直し」をモットーにタメになる面白い雑学や勉強コンテンツを
毎日作成するのでけいタンのブログを嫌になるくらい応援してくださいね!
今回の問題ジャンルについて
では、話題を元に戻しましょう。
今回は数Ⅲのド・モアブルと複素数平面の問題を行います。
前回同様、数Ⅲの複素数平面の問題なので高校生の方であれば、
理系の方にしかご縁がありませんが、いい問題を持ってきました。
なので、解くことや考えることだけでもいいので10分間だけお時間をください。
そして、理系の方で、複素数平面が苦手な方も数Ⅲが苦手な方も、
そもそも数学が苦手な方も数学ができるようになるきっかけの一つとなれるよう頑張りましょう!
・合わせて読みたい前回の関連記事:高校数学第5回~数Ⅲ正三角形と複素数平面~043(数学⑥) (keitan-zatsugaku.com)
↑複素数平面と正三角形の意外と考えないといけない問題です。
この記事を見てくれている方には必見のコンテンツになるでしょう!!
SoftBankへの乗り換えなら【ケータイ乗り換え.com】
![]()
では早速、複素数平面の問題を見ていきましょう!
今回の問題~数Ⅲド・モアブルと複素数平面(難易度☆☆☆…やや難)
今回は画像で問題を示します。

問題解決のためのヒント
もちろんその人の学力レベルや演習量で、難しいと感じる方もいれば、
いや、全然簡単だったけど…という方もいるかと思います。
(1)では、1+i/√3+iを極形式で表してみましょう。
そして、ド・モアブルの法則を利用してみましょう。
実数になるための条件というのは言い換えれば、
虚数の部分が0になることと同値ですね。
すなわち、先ほど極形式で表した虚数部分であるi*sinθ=0になるような、
角度θを求めるようにすれば、必然とnの値も出てくるでしょう。
(2)についてはまずは、式を少し変形する必要がありますね。
1/zが非常に扱いずらいので、両辺全体にzをかければいいですよね。
そうすれば、zの2次方程式ができるかと思います。
その方程式を解きましょう。そして、(1)と同様に、
解としてできてたzを極形式で表してみましょう。
後は、ド・モアブルの法則をうまく使えることができれば、求めたい値が出せるでしょう。
問題の解答
毎度のこと自分なりに分かりやすく手書きで作った回答を画像で示します。
一度自分なりにある程度解いてから、答えを確認するとより理解が深まりますよ。

(2)については以下にその続きがあります。
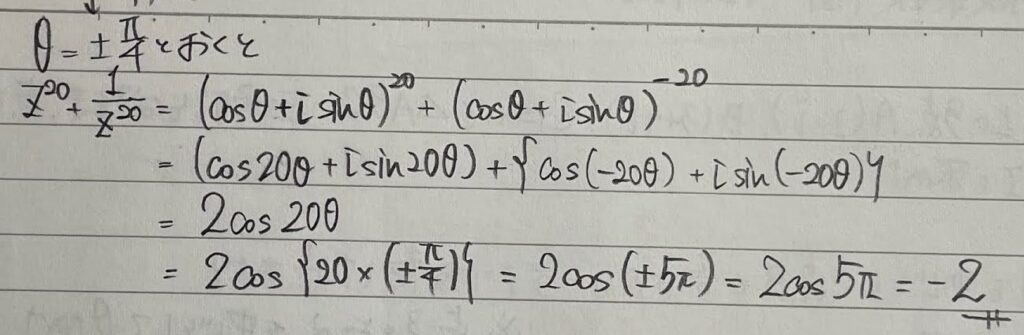
どのような過程で問題を解いているのかをしっかりと確認してくださいね!
まとめ~できないところを何度も演習しよう!
どうだったでしょうか。
しっかり考えないと解けない問題だったと思います。
大切なことは実際に問題を解いてみて、どこが分からないのか。どこができないのか…
というように、いろいろ自分なりに考えて、そして自分の手で計算を行うことが何より、
数学ができるようになるための一つのステップなのです。
あと、最後まで解けた方は複素数平面のド・モアブルの法則については大丈夫なので、
この調子でほかの分野についても頑張っていきましょう!
また、最後まで解けなかった方も今回をいい機会としていろいろ自分なりに復習してほしいと思います。
あきらめずにコツコツ学習することが最短の学力向上につながります!
今回の内容で少しでもタメになると感じてくれたら嬉しいです。
そして、
面白い・タメになると思った方は、いいね!とシェアによるこのブログの拡散をお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では、今回はここまでにします。
最後まで見ていただきありがとうございました。
また、明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
・合わせて読みたい前回の関連記事:高校数学第5回~数Ⅲ正三角形と複素数平面~043(数学⑥) (keitan-zatsugaku.com)
↑複素数平面と正三角形の意外と考えないといけない問題です。
この記事を見てくれている方には必見のコンテンツになるでしょう!!


