こんにちは、けいタンです。
今日は高校数学の問題演習を行います。
今回の問題ジャンルについて
今回は「数Ⅲの基本的な微分計算(その1)」という問題をします。
数Ⅲのメインといえば、言わずもがな「微分積分」だと思います。
そこで、今回は数Ⅲの初歩的な簡単な、でも基本的な要素が含まれている計算問題を準備しました。
何回も言いますが、基本的な微分計算を取り上げますので、
数Ⅲの微分計算が苦手な方も嫌いな方も、数学が得意になりたい方も
考えるだけでもいいので、問題を見てみてぜひ、チャレンジしてみてください!!
それが数学ができるようになるきっかけの一つとなれるかもしれませんからね!
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学演習第10回~数Ⅱ 因数定理と高次方程式
↑3次方程式や4次方程式といった高次方程式を扱っていきます。そのための解法として基本的な置換や因数定理の考え方にも触れていきます!

・合わせて読むべき関連記事:高校数学第6回~数Ⅲド・モアブルと複素数平面
↑ここでは、数Ⅲのド・モアブルと複素数平面の問題について取り上げます。数学が苦手な方や得意になりたい方は一度、見てほしいと思います。
・合わせて読むべき関連記事:高校数学第1回~数Ⅰ2次関数の場合分け
↑ここでは、数学の登竜門的な「2次関数の基本的な場合分け」について見ていきます。場合分けの考え方が分かりますので、まずは問題を解こう!
外出せず3時間で履歴書に書ける資格がとれる!伝え方コミュニケーション検定
![]()
↑自己肯定感が上がれば、自分の未来や将来の生き方が良くなるかも…
とにかく、ネガティブな考えよりもポジティブでありたいものですよね!
では早速、基本的な微分計算の問題について見ていきましょう!
今回の問題~数Ⅲ 基本的な微分計算(その1)(難易度☆…簡単)
問題:数Ⅲー基本的な微分計算(その1)
次の関数を微分せよ。
- y=(2x-1)(x²-x+3)
- y=2x-3/x²+1 (/は割り算を表す)
- y=1/(2x-3)²
- y=(3x+1)²(x-2)³
↑初心者からAIエンジニアになりたい方必見のオンラインAIプログラミングスクールです。
プログラミングも小学校で必修になりましたし、今からでもプログラミングを学習してみませんか?
問題解決のためのヒント
積の微分のおさらい
まずは、1番から見ていきましょう。
1番を展開してから、微分しても良いのですが、ここでは「積の微分」の計算方法で解きましょう。
1番の問題では、y=(2x-1)(x²-x+3) というようにy=(xの関数)×(xの関数)となっていますね。
つまり、積の形になっています。
このような積の形では、「積の微分」の計算方法が利用できます。
積の微分の公式は、 y’=f(x)’g(x)+f(x)g(x)’ ですが、
簡単に言い換えると、
y’=(最初の関数の微分)(後の関数そのまま)+(最初の関数そのまま)(後の関数の微分)
となります。
とにかく、「習うより慣れよ」の精神で、まずは計算してみてください!
商の微分のおさらい
2番・3番については「商の微分」の公式が使えそうです。
商の微分の公式は、y’={f(x)’g(x)-f(x)g(x)’}/{g(x)}² ですが、
こちらも積の微分と同様に、簡単に言い換えると、
y’=(分子の関数の微分)(分母の関数そのまま)-(分子の関数そのまま)(分母の関数の微分)÷(分母のそのままの関数)の2乗
になります。
例えば2番では、
(分子の関数の微分)=2
(分母の関数そのまま)=x²+1
(分子の関数そのまま)=2x-3
(分母の関数の微分)=2x
(分母のそのままの関数)の2乗=(x²+1)²
になります。
あとはこの式を整理すれば、OKというわけですね。
3番も同じように「商の微分」の計算公式を使って頑張ってください。
ちなみに確認ですが、定数の微分=0なので、くれぐれもご注意を。
中身微分の考え方
最期に4番です。
4番は積の微分で微分を行いますが、1点注意しないといけないことがあります。
それは、「中身微分の考え方」が必要だということです。
中身微分とは、どういうことかというと、
y=(3x+1)²(x-2)³を微分するときに、積の微分の考え方で
まず、(3x+1)²を微分しますね。これを微分すると2(3x+1)となります。
しかし、これで微分を終わってはいけません。
()の中身である(3x+1)についても微分しないといけないからです。
つまり、2(3x+1)ではなく、2(3x+1)×3なのです。
これが、中身微分の考え方です。
意外とこの「中身微分の考え方」は忘れやすいので、気を付けて微分してください!
問題の解答
毎度のこと自分なりに分かりやすく手書きで作った解答を画像で示します。
一度自分なりにある程度解いてから、答えを確認するとより理解が深まりますよ。
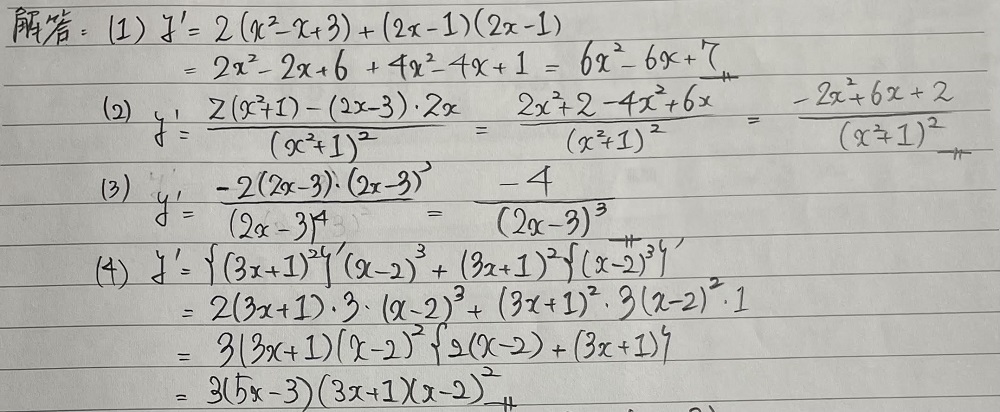
どのような過程で問題を解いているのかをしっかりと確認してくださいね!
まとめ~他の問題もいろいろ解いてみよう!
皆さん、やってみてどうだったでしょうか。
今回は積の微分・商の微分・中身微分の考え方が分かれば、
確実に解けた問題だったと思います。
とにかく、大切なことは実際に問題を解いてみて、どこが分からないのか。どこができないのか…
というように、いろいろ自分なりに考えて、そして自分の手で問題を解くことが何より、
数学ができるようになるための一つのステップになります。
とにかく、いろいろ自分なりに復習してほしいと思います。
あきらめずにコツコツ継続して学習することが最短の学力向上につながります!
「急がば回れ」の考え方ですよ~!
いいね!とシェアによるこのブログの拡散をお願いします!
今回の内容で少しでも面白い・タメになると感じてくれたら嬉しいです。
そして、
面白い・タメになると思った方は、いいね!とシェアによるこのブログの拡散をお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では、今回はここまでにします。
最後まで見ていただきありがとうございました。
![]()
↑なんと現在、こどもちゃれんじ・進研ゼミ小学/中学/高校講座にて「4月号、実質無料キャンペーン」を開催しているそうです!!このチャンスを逃すな!!
気になる方はチェックして内容を確認するだけでもしてみよう。
また、明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学演習第10回~数Ⅱ 因数定理と高次方程式
↑3次方程式や4次方程式といった高次方程式を扱っていきます。そのための解法として基本的な置換や因数定理の考え方にも触れていきます!
・合わせて読むべき関連記事:高校数学第6回~数Ⅲド・モアブルと複素数平面
↑ここでは、数Ⅲのド・モアブルと複素数平面の問題について取り上げます。数学が苦手な方や得意になりたい方は一度、見てほしいと思います。
・合わせて読むべき関連記事:高校数学第1回~数Ⅰ2次関数の場合分け
↑ここでは、数学の登竜門的な「2次関数の基本的な場合分け」について見ていきます。場合分けの考え方が分かりますので、まずは問題を解こう!



コメント