こんにちは、けいタンです。
今日も高校数学の問題演習を行います。
今回の問題ジャンルについて
今回は前回に引き続いて「数Ⅲの基本的な微分計算(その2)」という問題をします。
前回にも同じことを言いましたが数Ⅲのメインといえば、言わずもがな「微分積分」だと思います。
そこで、数Ⅲの初歩的な簡単な、でも基本的な要素が含まれている計算問題を準備しました。
何回も言いますが、基本的な微分計算を取り上げますので、
数Ⅲの微分計算が苦手な方も嫌いな方も、数学が得意になりたい方も
考えるだけでもいいので、問題を見てみてぜひ、チャレンジしてみてください!!
それが数学ができるようになるきっかけの一つとなれるかもしれませんからね!
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学~数Ⅲ 基本的な微分計算(その1)
↑数Ⅲの基本的な微分問題を解くことで、積の微分・商の微分・中身微分の考え方を再定着させましょう!簡単な問題なので、5分でできますよ~!

・合わせて読むべき関連記事:高校数学~数Ⅲド・モアブルと複素数平面
↑ここでは、数Ⅲのド・モアブルと複素数平面の問題について取り上げます。数学が苦手な方や得意になりたい方は一度、見てほしいと思います。
・合わせて読むべき関連記事:高校数学~数Ⅰ三角比と基本定理
↑数学が苦手な方も嫌いな方でも取り組めるような基本的な問題をご紹介します。数学が得意になりたい方、好きになりたい方は必見です。
では早速、基本的な微分計算の問題について見ていきましょう!
今回の問題~数Ⅲ 基本的な微分計算(その2)(難易度☆…簡単)
問題:数Ⅲー基本的な微分計算(その2)
次の関数を微分せよ。
- y=cos(2x+3)
- y=cosx/3+sinx
- y=log|tanx| (||は絶対値を表す)
- y=exsinx
↑初心者からAIエンジニアになりたい方必見のオンラインAIプログラミングスクールです。
プログラミングも小学校で必修になりましたし、今からでもプログラミングを学習してみませんか?
問題解決のためのヒント
復習~中身微分の考え方
まずは1番から見てみましょう。
この問題では、cosxを微分したら、-sinxになることと
前回にも出てきましたが、中身微分の考え方が分かれば解くことができるでしょう。
中身微分の考え方については、前回の記事を参照ください。
※前回の投稿記事:高校数学演習第11回~数Ⅲ 基本的な微分計算(その1)
↑積の微分や商の微分・中身微分の考え方について自信がない方は、こちらから確認してみるといいと思います。
三角関数と対数関数の微分
2番は商の微分の考え方でいいので、説明しなくても大丈夫でしょう。
ちなみに、sinxを微分したら、cosxになりますからね。
では次は、3番の問題です。
3番の問題では、y=log|tanx|の微分になりますが、
こちらは、logの微分したものと、中身微分であるtanxを微分したものが何なのか分かれば、
解けると思います。
logは「分の1」すなわち、例えばlogxだったら、1/xという感じに、「分の1」の形になります。
なので、log|tanx|だったらどうなるのか?これはもう分かったはずです。
あと、tanxを微分したものは1/cos²xになります。
この際に確認しておきましょう。
ネイピア数exの微分
最後に4番です。これも説明がいるのか、と思いたくなるようなレベルの問題ですね。
というものネイピア数exの微分は、変わらずexのままです。
そしてあとは、4番は積の微分が使えるので、もう解けたも同然ですね!
問題の解答
毎度のこと自分なりに分かりやすく手書きで作った解答を画像で示します。
一度自分なりにある程度解いてから、答えを確認するとより理解が深まりますよ。
画像では、(5)~(8)と表記されていますが、(5)が今回の問題の(1)に相当します。
以下、同じようにして確認してくださいね。
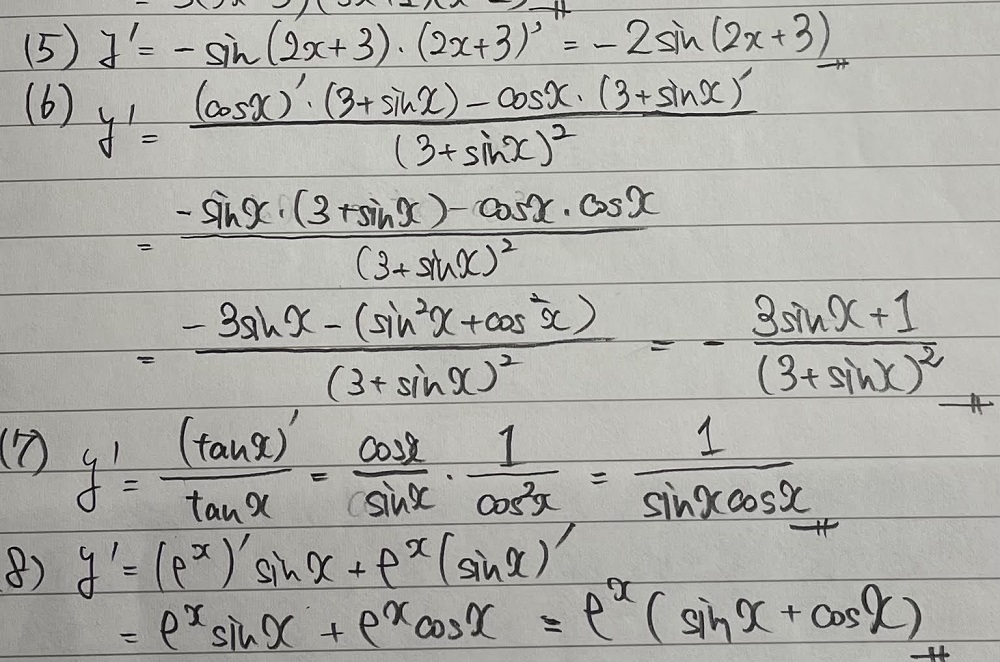
どのような過程で問題を解いているのかをしっかりと確認してくださいね!
まとめ~他の問題もいろいろ解いてみよう!
皆さん、やってみてどうだったでしょうか。
今回は中身微分の考え方や三角関数と対数関数・exの微分が分かれば、
確実に解けた問題だったと思います。
とにかく、大切なことは実際に問題を解いてみて、どこが分からないのか。どこができないのか…
というように、いろいろ自分なりに考えて、そして自分の手で問題を解くことが何より、
数学ができるようになるための一つのステップになります。
とにかく、いろいろ自分なりに復習してほしいと思います。
あきらめずにコツコツ継続して学習することが最短の学力向上につながります!
「急がば回れ」の考え方ですよ~!
いいね!とシェアによるこのブログの拡散をお願いします!
今回の内容で少しでも面白い・タメになると感じてくれたら嬉しいです。
そして、
面白い・タメになると思った方は、いいね!とシェアによるこのブログの拡散をお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では、今回はここまでにします。
最後まで見ていただきありがとうございました。
また、明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学~数Ⅲ 基本的な微分計算(その1)
↑数Ⅲの基本的な微分問題を解くことで、積の微分・商の微分・中身微分の考え方を再定着させましょう!簡単な問題なので、5分でできますよ~!
・合わせて読むべき関連記事:高校数学~数Ⅲド・モアブルと複素数平面
↑ここでは、数Ⅲのド・モアブルと複素数平面の問題について取り上げます。数学が苦手な方や得意になりたい方は一度、見てほしいと思います。
・合わせて読むべき関連記事:高校数学~数Ⅰ三角比と基本定理
↑数学が苦手な方も嫌いな方でも取り組めるような基本的な問題をご紹介します。数学が得意になりたい方、好きになりたい方は必見です。



コメント