こんにちは、けいタンです。
今回は月1回の意外と大好評の「数学パズル」をやります。
今回のテーマについて
実のところ「数学パズル」は人気があります。
このことは多くの方にとって「数学パズルは面白い、やってみたい」という感情の表れだと思います。
けいタンとしてもこれからも、より多くの人に数学の面白さを伝えていきたいので、
とても嬉しい知らせになります。
今日は「解けたら気持ちいい数学パズル」を紹介します。
”解けたら気持ちいい”ので皆さんも果敢に挑戦してみてくださいね!
前もってちょっとしたヒントとしていっておきますが、
問題の条件をしっかりと理解して、あなたの柔軟な発想や最後まで丁寧に数を数えられることこそが、
今回の問題を解くカギとなるでしょう。
では早速ですが、始めていきましょう!
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学演習第15回~数Ⅱ 点と直線の距離と三角形
↑高校数学の中でも、なかなか覚えづらく理解しづらい「点と直線の距離」の公式を用いた図形と方程式の問題を持ってきましたので、5分で解いて見てください!

・合わせて読むべき関連記事:数学パズル第4回~考えたら分かる組み合わせパズル
↑すぐには答えはわからないけど、よくよく考えたら分かるのが数学パズルの面白いところ!そんなよく考えたら分かる組み合わせパズルを紹介します!
・合わせて読むべき関連記事:数学パズル第3回~意外と解けない虫食い算に挑め!
↑分かっている情報から分からないところを推測して解く虫食い算に挑戦してみませんか?地味に好評の数学パズル第3弾!
では実際に、解けたらとても気持ちいい数学パズルに挑戦してみましょう!
第1問:増える昆虫X
ある昆虫Xの成虫は、1日に子供を1匹生みます。
2日経つとその子供は成虫になります。
そして成虫になった昆虫Xは翌日から子供を生み始め、それ以降毎日子供を1匹生みます。
なお、昆虫Xのオス・メスの区別はなしとして、すべての成虫が子供を生むことができるとします。
では、1日目に成虫の昆虫Xが1匹いたとすると、
10日目には何匹(子供・成虫合わせて)になるのでしょうか?
ただし、この10日間のうちに死んでしまう昆虫Xはいないとします。
↑U-Nextでは無料トライアルを実施しています!
映画やドラマ・アニメがお好きな方はここからチェックしてみましょう!
この問題の解答
正解は41匹です。
1日1日、1匹1匹、間違えることなく数えることができたでしょうか。
それぞれの個体数などの詳細については以下のようになるはずです。
間違えた方は確認してみてください。
- 1日目:成虫×1,子供×0,成虫になる前日の子供×0
- 2日目:成虫×1,子供×1,成虫になる前日の子供×0
- 3日目:成虫×1,子供×1,成虫になる前日の子供×1
- 4日目:成虫×2,子供×1,成虫になる前日の子供×1
- 5日目:成虫×3,子供×2,成虫になる前日の子供×1
- 6日目:成虫×4,子供×3,成虫になる前日の子供×2
- 7日目:成虫×6,子供×4,成虫になる前日の子供×3
- 8日目:成虫×9,子供×6,成虫になる前日の子供×4
- 9日目:成虫×13,子供×9,成虫になる前日の子供×6
- 10日目:成虫×19,子供×13,成虫になる前日の子供×9
第2問:点と線の問題
下の図のように、9個の点が格子状に配置されています。
一筆書きですべての点を通る、何回か折れ曲がった直線を考えるとき、
もっとも曲がる回数が少なくなるようにするにはどのようにしたらよいでしょうか?

ヒント:最短の折れ曲がりの回数は「3回」になります。
「4回」になってしまう方はもっと柔軟に考えてみて!
↑電子書籍で漫画を見たい方にはおススメですよ~!
この問題の解答
解答は下の図のようになります。
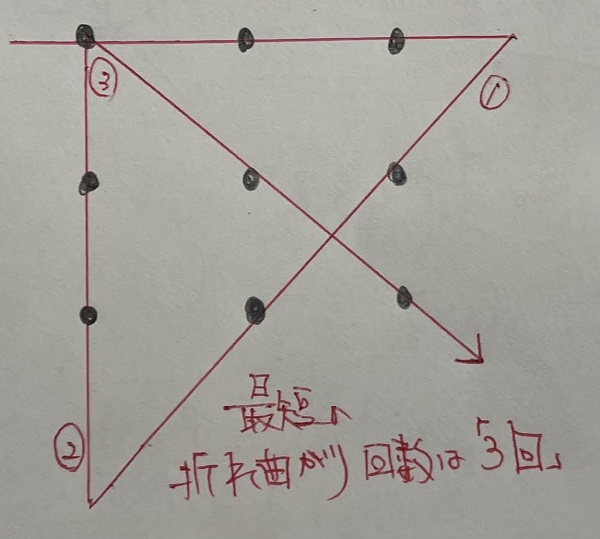
この問題を解くポイントは、「点が整列した領域の外側へと直線をのばすこと」に
気づけるかどうかだと思います。
そのようにして考えると最短の折れ曲がり回数は「3回」で一筆書きができますね。
まとめ~柔軟な発想でパズルを攻略せよ!
いかがだったでしょうか。
簡単に解けたかたもいれば、思ったよりも苦戦した方もいたのではないでしょうか。
解けなくても自分なりにいろいろ考えることが、数学パズルの醍醐味ですよね。
このような比較的誰でも考えることができる
面白い数学パズルの問題をたまに取り上げるつもりなのでお楽しみにしていてくださいね!
いいね!とシェアによるこのブログの拡散をお願いします!
そして今回の内容で少しでも皆さんが面白い・タメになると感じてくれたら嬉しいです。
あと最後に、
面白い・タメになると思った方は、いいね!とシェアによるこのブログの拡散をお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
それでは今日はここまでとします。最後まで見ていただきありがとうございました。
では、また明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学演習第15回~数Ⅱ 点と直線の距離と三角形
↑高校数学の中でも、なかなか覚えづらく理解しづらい「点と直線の距離」の公式を用いた図形と方程式の問題を持ってきましたので、5分で解いて見てください!
・合わせて読むべき関連記事:数学パズル第4回~考えたら分かる組み合わせパズル
↑すぐには答えはわからないけど、よくよく考えたら分かるのが数学パズルの面白いところ!そんなよく考えたら分かる組み合わせパズルを紹介します!
・合わせて読むべき関連記事:数学パズル第3回~意外と解けない虫食い算に挑め!
↑分かっている情報から分からないところを推測して解く虫食い算に挑戦してみませんか?地味に好評の数学パズル第3弾!


