こんにちは、けいタンです。
今回は20回目となる科学の電柱に関する話について考えていきましょう。
今回のテーマについて
知らない方がいるかと思いますが、
道端に立っている電柱は中身が空洞で、丸いパイプ状になっています。
ではここで、皆さんに伺いましょう。
なぜ、電柱の中は空洞なのでしょうか?
この疑問に答えられる方はそう多くいないかと思います。
そこで今回のテーマは、
どうして電柱の中は空洞になっているのか?
という、知らない方が多いテーマについて、
科学的な観点からその原因を追究していきましょう!
では、Let’s science!(サイエンス!)
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:集中と分散~ヒールで踏まれるとすごく痛い理由
↑ハイヒールで足を踏まれるとものすごく痛い!なんで普通の靴よりもハイヒールで踏まれた方が痛いのか?…それは力に集中と分散が関係しているようです。

・合わせて読むべき関連記事:角運動量~なぜフィギュアスケート選手は高速回転できるのか
↑フィギュアスケートの選手が高速スピンできるのはどうしてでしょうか?どうやら「角運動量保存の法則」というのが関係しそうです…。
・合わせて読むべき関連記事:慣性力~車や電車で起こるあの不思議な現象を理解する
↑あなたの身の回りに起きている不思議な現象の1つは慣性力の仕業かもしれません。今回を機に慣性力とは何かを知っておこう!
ではまずは、今回の話の結論部分から始めていきます。
今回のテーマに対する解答
どうして電柱の中は空洞になっているのか?
という疑問に対する簡単な模範解答は、
モノの強度を示す断面係数という値が、空洞でもほとんど変わらないことにあります。
では断面係数について、もう少しだけ詳しく見ていくことにしましょう。
空洞でも曲げに対する強さはほとんど変わらない!

断面係数と中空材
こんな話をすると「へえ~意外」と感じる(言う)方がよくいるのですが、
実は、中身が仮にコンクリートで詰まった電柱と中身が空洞であるパイプ状の電柱では、
曲げに対する強さはあまり変わらないのです。
そうです、多くの方が中身が空洞であるパイプ状の電柱よりも、
中身がコンクリートで詰まった電柱のほうが、丈夫で曲げに対する耐性も大きいと思われるのですが、
曲げに対する強さは、コンクリートで詰まっていても空洞だとしてもあまり変わらないのです。
そして、曲げる力(物理学では「曲げモーメント」といいます)に対する強さや抵抗力を
「断面係数」というのです。
また、中身が詰まった円筒を中実材、中身が空洞のパイプのようなものを中空材といいます。
断面係数に関する数式

ちなみにですが、中実材と中空材の断面係数はそれぞれ以下のような数式で求めることができます。
〇中実材(円筒)の断面係数:Z1=π/32×(直径)3
〇中空材(パイプ)の断面係数:Z2=π/32×{(外径)4-(内径)4/外径}
何かややこしい式ですね… 特に中空材(パイプ)の断面係数のほうが(笑)
まあ、この公式を覚える必要はまったくもってありませんので、
リラックスしてこの話を見てください。
では話の続きをしていきます。
パイプの内径と同じ直径の円筒と、内径の1割の厚みを持ったパイプの断面係数を比較すると、
Z1:Z2=1:0.89 となります。
これはどんなことを意味しているのかというと、
パイプは円筒のおおよそ90%の曲げ強さを持ち、
この場合の例では、中身が詰まっていても空洞でも、あまり強度は変わらないといえるでしょう。
強度が大きく変わらない理由
では、強度が中身がコンクリートで詰まっていても、中身が空洞のパイプ状であっても
あまり変わらないのはどうしてでしょうか?
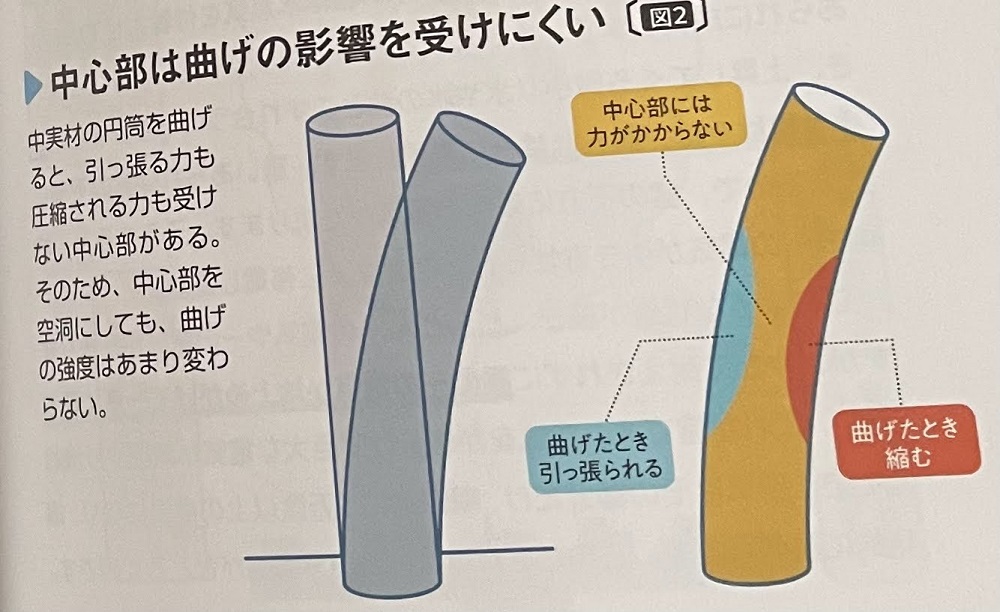
このように強度が大きく変わらない理由は、電柱のような円筒を曲げたとき、
曲げた外側の方は引っ張られ、内側の方は圧縮されますが、
円筒の中心部には引っ張りも圧縮も受けない部分が生じます。
つまり、曲げの強度に関しては、中心部は影響しないのです。
また、下の図の参考程度に見ていただけると、
先ほどの強度が大きく変わらない理由が視覚的に分かりやすいかと思います。
まとめ~中が空でも断面係数はほとんど同じ!
いかがだったでしょうか。
では今回も、最後にまとめをして終わりにしましょう。
確認しておくべき電柱と断面係数に関する5つのこと
- 中身がコンクリートで詰まった電柱と中身が空洞であるパイプ状の電柱では、曲げに対する強さはあまり変わらない
- 曲げる力(曲げモーメント)に対する強さや抵抗力を断面係数という
- 中身が詰まった円筒を中実材、中身が空洞のパイプのようなものを中空材という
- パイプの内径と同じ直径の円筒と、内径の1割の厚みを持ったパイプの断面係数を比較すると、Z1:Z2=1:0.89 となる
→パイプは円筒のおおよそ90%の曲げ強さを持ち、この場合では、中身が詰まっていても空洞でも、あまり強度は変わらないといえる - 強度が大きく変わらない理由は、電柱のような円筒を曲げたとき、曲げた外側の方は引っ張られ、内側の方は圧縮されるが、円筒の中心部には引っ張りも圧縮も受けない部分が生じるからである
→つまり、曲げの強度に関しては、中心部は影響しない
いいね!とシェアによるこのブログの拡散をお願いします!
今回の内容で少しでも面白い・タメになると感じてくれたら嬉しいです。
そして、
少しでも面白い・タメになると思った方は、いいね!とシェアをお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では今日はここまでです。最後までご覧くださりありがとうございました。
また明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:集中と分散~ヒールで踏まれるとすごく痛い理由
↑ハイヒールで足を踏まれるとものすごく痛い!なんで普通の靴よりもハイヒールで踏まれた方が痛いのか?…それは力に集中と分散が関係しているようです。

・合わせて読むべき関連記事:角運動量~なぜフィギュアスケート選手は高速回転できるのか
↑フィギュアスケートの選手が高速スピンできるのはどうしてでしょうか?どうやら「角運動量保存の法則」というのが関係しそうです…。
・合わせて読むべき関連記事:慣性力~車や電車で起こるあの不思議な現象を理解する
↑あなたの身の回りに起きている不思議な現象の1つは慣性力の仕業かもしれません。今回を機に慣性力とは何かを知っておこう!


コメント