こんにちは、けいタンです。
今日も高校数学の問題演習を行います。
今回の問題ジャンルについて
今回は「数Ⅲ~基本的な極限値の計算」という問題をします。
数Ⅲの問題になるので、多少は難易度が上がりますが、
数Ⅲ全体で見ればタイトルにもある通り基本的な問題だといえるでしょう。
また、この問題は極限に関する問題で、その中でも代表的な極限値を求める問題となっています。
といっても今回の問題は、数Ⅲの比較的簡単な、
でも基本的な大事な考え方の要素が含まれている極限値を求める問題になります。
なので、理系の方をメインに、数Ⅲの極限が苦手な方も嫌いな方も、数学が得意になりたい方も
考えるだけでもいいので、問題を見てみてぜひ、チャレンジしてみてください!!
それが数学ができるようになるきっかけの一つとなれるかもしれませんからね!
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学第16回~数Ⅱ 3点の座標と円の方程式
↑3点の座標と円の方程式に関する高校数学の問題を練習しよう!この問題では、ある解法が分かれば、後はただただ計算するだけで解ける問題なんですよ…

・合わせて読むべき関連記事:高校数学第12回~数Ⅲ 基本的な微分計算(その2)
↑数Ⅲの基本的な微分問題を解くことで、三角関数と対数関数の微分を再定着させましょう!簡単な問題なので、5分でできますよ~!
・合わせて読むべき関連記事:数学パズル第5回~解けたら気持ちいいパズル
↑数学パズルの醍醐味の一つは柔軟な思考力が鍛えられること!そんなことで今回は解けたら気持ちいい数学パズルをご紹介しましょう。
では早速、基本的な極限値を求める問題について見ていきましょう!
今回の問題~数Ⅲ 基本的な極限値の計算 (難易度☆☆…標準)
問題:数Ⅲー基本的な極限値の計算
以下の問いに答えよ。
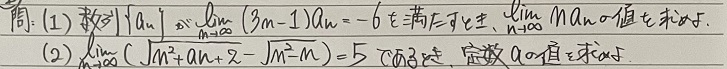
問題解決のためのヒント

1番の問題について
では、早速1番の問題のヒントである解き方(指針)を説明したいと思います。
数列{an}がlim(n→∞)(3n-1)an=-6を満たすとき、lim(n→∞)nanの値を求めよ
この問題をまず見たときに考えてほしいことは、
nanと(3n-1)anとの関係式を立てることです。
このときには、まだlim(n→∞)については考えなくても大丈夫です。
すなわち、nan=(3n-1)an × n/(3n-1)…というような等式を勝手に作ります。
そうすれば、両辺の式に対して極限を考えると、
lim(n→∞)nan = lim(n→∞)(3n-1)an × lim(n→∞)n/(3n-1)
となり、lim(n→∞)(3n-1)an=-6の条件から、求めるべき極限値lim(n→∞)nanの値が分かるでしょう。
2番の問題について
では次は2番の問題です。
lim(n→∞)(√n2+an+2-√n2-n)=5であるときのaの値を求めよ
この問題では、単にnを無限大に飛ばしても∞-∞(不定形)となり、求めたいaの値は分かりません。
では、どうすればよいか…そのための解法の1つが式変形にあります。
今回の場合、√n2+an+2-√n2-nというように、(ルートールート)という式になっているので、
分母分子に(ルート+ルート)をかけてあげて、ルートを外すように式変形をしましょう。
この式変形は、先ほどにも言ったように、極限値を求める問題で、不定形になってしまう場合に
行うべき操作の一つになります。
式変形をする問題は、大学入試でもよく見られますので、この機会にぜひ練習をしてみてはいかがでしょうか。
問題の解答
毎度のこと自分なりに分かりやすく手書きで作った解答を画像で示します。
一度自分なりにある程度解いてから、答えを確認するとより理解が深まりますよ。

どのような過程で問題を解いているのかをしっかりと確認してくださいね!
まとめ~他の問題もいろいろ解いてみよう!
皆さん、やってみてどうだったでしょうか。
今回は分かっている条件から関係式を立てたり、式を変形することが分かれば、
確実に解けた問題だったと思います。
とにかく、大切なことは実際に問題を解いてみて、どこが分からないのか。どこができないのか…
というように、いろいろ自分なりに考えて、そして自分の手で問題を解くことが何より、
数学ができるようになるための一つのステップになります。
とにかく、いろいろ自分なりに復習してほしいと思います。
あきらめずにコツコツ継続して学習することが最短の学力向上につながります!
「急がば回れ」の考え方ですよ~!
いいね!とシェアによるこのブログの拡散をお願いします!
今回の内容で少しでも面白い・タメになると感じてくれたら嬉しいです。
そして、
面白い・タメになると思った方は、いいね!とシェアによるこのブログの拡散をお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では、今回はここまでにします。
最後まで見ていただきありがとうございました。
また、明日お会いしましょう。けいタン
※過去の投稿一覧(ブログ)
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:高校数学第16回~数Ⅱ 3点の座標と円の方程式
↑3点の座標と円の方程式に関する高校数学の問題を練習しよう!この問題では、ある解法が分かれば、後はただただ計算するだけで解ける問題なんですよ…
・合わせて読むべき関連記事:高校数学第12回~数Ⅲ 基本的な微分計算(その2)
↑数Ⅲの基本的な微分問題を解くことで、三角関数と対数関数の微分を再定着させましょう!簡単な問題なので、5分でできますよ~!
・合わせて読むべき関連記事:数学パズル第5回~解けたら気持ちいいパズル
↑数学パズルの醍醐味の一つは柔軟な思考力が鍛えられること!そんなことで今回は解けたら気持ちいい数学パズルをご紹介しましょう。



コメント