こんにちは、けいタンです。
ここでは、高校数学の問題演習を行います。
扱う問題ジャンルは何なのか?
今回は「数Ⅰ~三角比と式の値」という問題をします。
与えられた条件から式をうまく変形して、求める式の値を出せるかどうかが問われる問題です。
そして同時に、三角比の基本的な考え方の要素が含まれている問題でもあります。
したがって、数Ⅰの三角比が苦手な方も嫌いな方も、数学が得意になりたい方も
考えるだけでもいいので、問題を見てみてぜひ、チャレンジしてみてください!!
それが数学ができるようになるきっかけの一つとなれるかもしれませんからね!
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:数学パズル第6回~少しややこしいナンプレとバトル!
↑数学パズルの定番であるナンプレを今回、紹介します。その名も「少しだけややこしいハート形ナンプレ!」。挑戦者をお待ちしています。

・合わせて読むべき関連記事:高校数学演習第7回~数Aじゃんけんと確率
↑普段何気なくやっている「じゃんけん」には確率の考えが隠れています。確率のセンスを磨けるよう「じゃんけんと確率」の問題にチャレンジ!
・合わせて読むべき関連記事:高校数学第1回~数Ⅰ2次関数の場合分け
↑みんなで2次関数の基本的な場合分け問題を解こう!
では早速、基本的な三角比と式の値の問題について見ていきましょう!
今回の問題~数Ⅰ 三角比と式の値(難易度☆☆…標準)
問題:数Ⅰー三角比と式の値
以下の問いに答えよ。
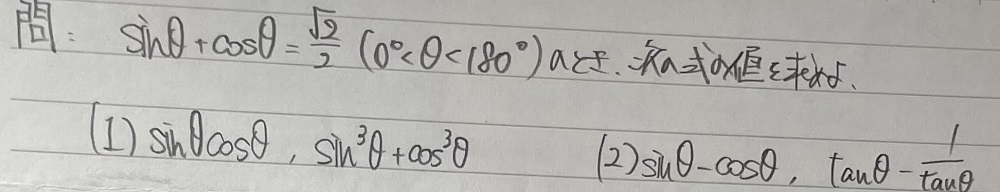
問題解決のためのヒント

1番の問題について
まずは、問題の条件を把握しておきましょう。
sinθ+cosθ=√2/2のとき(0<θ<π)、sinθcosθとsin3θ+cos3θの値を求めよ
サインとコサインの和が与えられて、そこから積を導くためには、式を2乗すればよいでしょう。
すなわち、(sinθ+cosθ)2=sin2θ+2sinθcosθ+cos2θ=1/2となりますね。
ここで、三角比の基本定理の1つであるsin2θ+cos2θ=1を用いれば値を出すことができます。
sin3θ+cos3θの値に関しては、3条の基本対称式x3+y3=(x+y)(x2-xy+y2)を使って、
x=sinθ、y=cosθと考えれば、大丈夫でしょう!
2番の問題について
sinθ-cosθとtanθ+1/tanθの値を求めよ…
まず、sinθ-cosθについては、(sinθ-cosθ)2=1-2sinθcosθなので、これにルートを乗せた値が求める答えになりますが、
問題なのは解が正なのか負なのかということです。
これについては、問題の条件を見るとθは0°から180°までの範囲をとるので、sinθが必ず正であることが分かります。
これと1番の問題から(sinθcosθ<0)、cosθが負であることが分かるため、
結果として、sinθ-cosθは正の値をとることになります。
tanθ+1/tanθに関しては、ちょっとした式変形をすればいいので、ノーヒントで頑張ってください!
問題の解答
毎度のこと自分なりに分かりやすく手書きで作った解答を画像で示します。
一度自分なりにある程度解いてから、答えを確認するとより理解が深まりますよ。
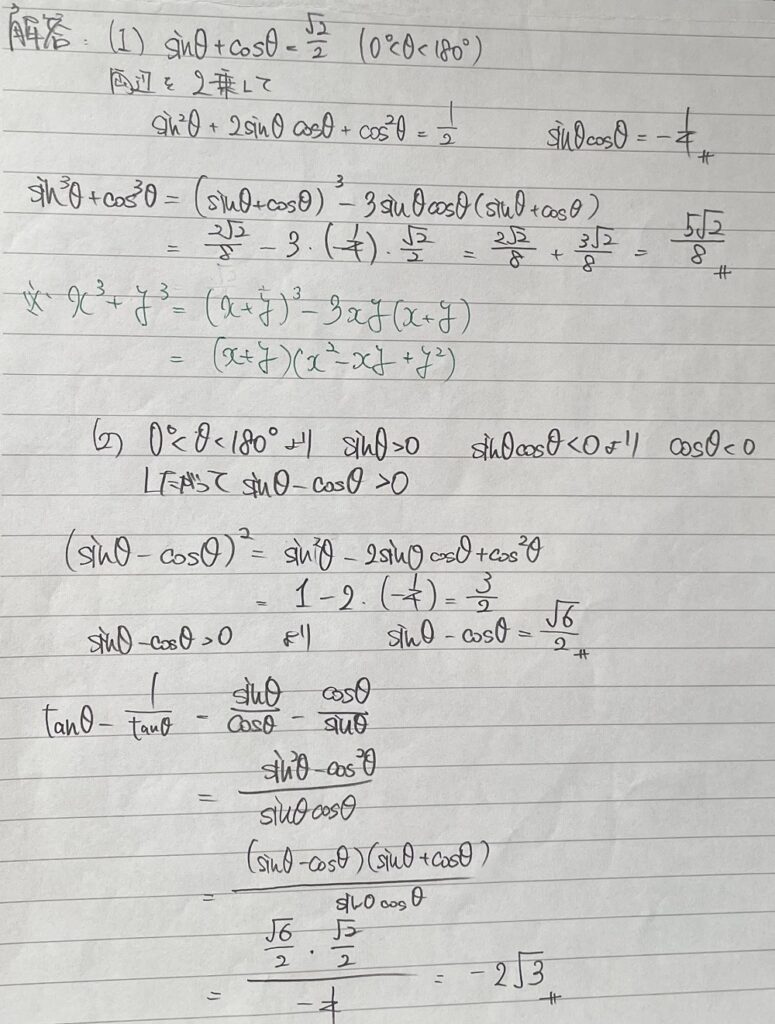
どのような過程で問題を解いているのかをしっかりと確認してくださいね!
まとめ~他の問題もいろいろ解いてみよう!
皆さん、やってみてどうだったでしょうか。
今回は三角比と基本公式とsinθ-cosθが正になることが分かれば、
解くことができた問題だったと思います。
とにかく、大切なことは実際に問題を解いてみて、どこが分からないのか。どこができないのか…
というように、いろいろ自分なりに考えて、そして自分の手で問題を解くことが何より、
数学ができるようになるための一つのステップになります。
とにかく、いろいろ自分なりに復習してほしいと思います。
あきらめずにコツコツ継続して学習することが最短の学力向上につながります!
「急がば回れ」の考え方ですね!
いいね!とシェアをお願いします!
今回の内容で少しでも面白い・タメになると感じてくれたら嬉しいです。
そして、
面白い・タメになると思った方は、いいね!とシェアをお願いします。
タメになるコンテンツ作成の大きな大きなモチベーションとなります。
では、今回はここまでにします。
最後まで見ていただきありがとうございました。
また、別の投稿でお会いしましょう。けいタン
※過去の投稿一覧(ブログ)
合わせて読むべき関連記事をチェック!
・合わせて読むべき前回の関連記事:数学パズル第6回~少しややこしいナンプレとバトル!
↑数学パズルの定番であるナンプレを今回、紹介します。その名も「少しだけややこしいハート形ナンプレ!」。挑戦者をお待ちしています。
・合わせて読むべき関連記事:高校数学演習第7回~数Aじゃんけんと確率
↑普段何気なくやっている「じゃんけん」には確率の考えが隠れています。確率のセンスを磨けるよう「じゃんけんと確率」の問題にチャレンジ!
・合わせて読むべき関連記事:高校数学第1回~数Ⅰ2次関数の場合分け
↑みんなで2次関数の基本的な場合分け問題を解こう!



コメント